https://www.acmicpc.net/problem/4883
4883번: 삼각 그래프
입력은 여러 개의 테스트 케이스로 이루어져 있다. 각 테스트 케이스의 첫째 줄에는 그래프의 행의 개수 N이 주어진다. (2 ≤ N ≤ 100,000) 다음 N개 줄에는 그래프의 i번째 행에 있는 정점의 비용이
www.acmicpc.net
문제
이 문제는 삼각 그래프의 가장 위쪽 가운데 정점에서 가장 아래쪽 가운데 정점으로 가는 최단 경로를 찾는 문제이다.
삼각 그래프는 사이클이 없는 그래프로 N ≥ 2 개의 행과 3열로 이루어져 있다. 삼각 그래프는 보통 그래프와 다르게 간선이 아닌 정점에 비용이 있다. 어떤 경로의 비용은 그 경로에서 지나간 정점의 비용의 합이다.
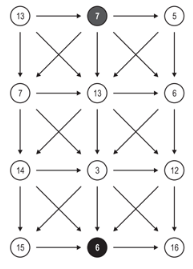
오른쪽 그림은 N = 4인 삼각 그래프이고, 가장 위쪽 가운데 정점에서 가장 아래쪽 가운데 정점으로 경로 중 아래로만 가는 경로의 비용은 7+13+3+6 = 29가 된다. 삼각 그래프의 간선은 항상 오른쪽 그림과 같은 형태로 연결되어 있다.
입력
입력은 여러 개의 테스트 케이스로 이루어져 있다. 각 테스트 케이스의 첫째 줄에는 그래프의 행의 개수 N이 주어진다. (2 ≤ N ≤ 100,000) 다음 N개 줄에는 그래프의 i번째 행에 있는 정점의 비용이 순서대로 주어진다. 비용은 정수이며, 비용의 제곱은 1,000,000보다 작다.
입력의 마지막 줄에는 0이 하나 주어진다.
출력
각 테스트 케이스에 대해서, 가장 위쪽 가운데 정점에서 가장 아래쪽 가운데 정점으로 가는 최소 비용을 테스트 케이스 번호와 아래와 같은 형식으로 출력한다.
k는 테스트 케이스 번호, n은 최소 비용이다.
코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class No4883 {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken()), tc = 1;
while (N != 0) {
int[][] dp = new int[N][3];
for (int i = 0; i < N; i++) {
st = new StringTokenizer(br.readLine());
dp[i][0] = Integer.parseInt(st.nextToken());
dp[i][1] = Integer.parseInt(st.nextToken());
dp[i][2] = Integer.parseInt(st.nextToken());
}
//첫번째행, 두번째행 초기화
dp[1][0] += dp[0][1];
dp[1][1] += Math.min(dp[1][0], Math.min(dp[0][1], dp[0][1]+dp[0][2]));
dp[1][2] += Math.min(dp[1][1], Math.min(dp[0][1], dp[0][1]+dp[0][2]));
//3~N번째행
for (int i = 2; i < N; i++) {
dp[i][0] += Math.min(dp[i - 1][0], dp[i - 1][1]);
dp[i][1] += Math.min(Math.min(dp[i][0], dp[i - 1][0]),
Math.min(dp[i - 1][1], dp[i - 1][2]));
dp[i][2] += Math.min(dp[i][1], Math.min(dp[i - 1][1], dp[i - 1][2]));
}
System.out.println(tc + ". " + dp[N - 1][1]);
tc++; //테스트 케이스 수 증가
N = Integer.parseInt(br.readLine());
}
}
}풀이
출발 지점이 무조건 위쪽 가운데 정점이기 때문에 첫번째 행과 두번째 행의 값은 직접 넣어주고 나머지는 규칙을 이용하여 넣어주면 된다.
'코딩테스트' 카테고리의 다른 글
| [그래프] 백준 16948번 데스 나이트 자바 (Java) (0) | 2023.02.06 |
|---|---|
| [그래프] 백준 5567번 결혼식 자바 (Java) (0) | 2023.02.05 |
| [그래프] 백준 11403번 경로 찾기 자바 (Java) (1) | 2023.02.05 |
| [최단경로] 백준 1504번 특정한 최단 경로 자바 (Java) (1) | 2023.02.03 |
| [최단경로] 백준 1753번 최단경로 자바 (Java) (0) | 2023.02.01 |




댓글